About My Profession

SAT Math Problem in 1982

 

Background

SAT 1982 Math Problem Everyone Got Wrong

At the right is a math problem that appeared on the 1982 Scholastic Aptitude Test (SAT) test. Normally, no one gets to see any SAT question as they're closely guarded. But this one came to light because the correct answer was not in the list of possible answers. It came to light because  three students complained to the SAT board that this question did not have the correcct answer! The SAT would have to admit their mistake and every SAT containing this question needed to be rescored.

You can read an article about it in Scientific American here.

So what does this have to do with me? Short answer, the problem came to me.

An Impromptu Question

Jim Martens, my uncle, was a pretty smart guy, but often far too arrogant for his own good. He knew he was smart and his proof was that he applied and was admitted to Mensa, a high IQ society. He acted like he was smarter than anybody and was too quick to belittle.

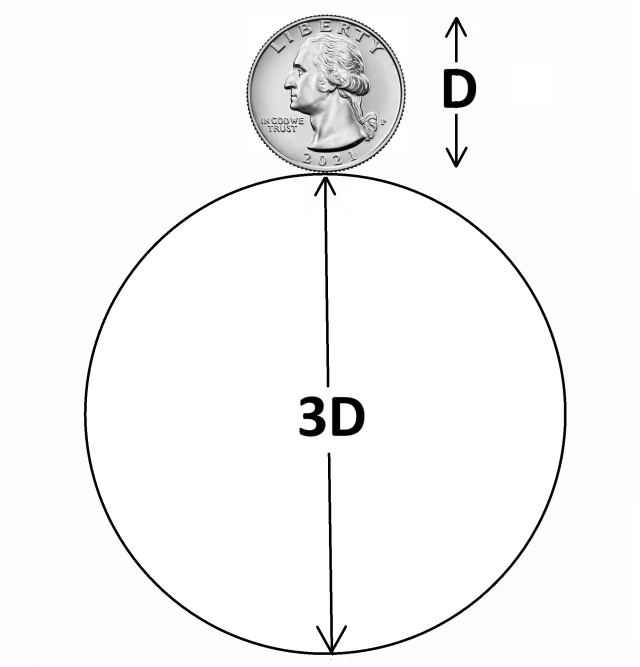
I had barely started the full time job at Computer Graphics and I saw the daily routine of Jim and his partner, Ron, as they went to lunch together everyday. One day in late May of 1982, Jim storms into my office as he's just heard of the SAT problem and he is stumped, simply not understanding the answer. My office was at the back of the building and I had a chalkboard so he describes the problem and draws it as shown in the diagram at the left. Note that one difference to the test was that he used a quarter (his was drawn crudely as you can imagine).

It is important to note that I had never seen this problem before so it was entirely new, like I was a student taking the SAT. When he finished the diagram he asks the question, "How many turns does the quarter make around the larger circle?" Of course, I can see instantly the answer is supposed to be 3.

Circumference of Quarter = 1Dπ

Circumference of Large Circle = 3Dπ

So calculating the ratio is simply 3Dπ/1Dπ and the D and the π cancels out so it's 3/1 or simply 3. But he's given me a bit of extra info that the test takers didn't have: that the answer 3 is not correct. On the other hand he didn't give me the multiple choices. I quickly in my mind started the rotation of the quarter and instantly knew the answer was going to be more than 3. And then it came to me and I said, "4!" It had taken me just seconds to figure it out and Jim was so pissed off! "How come the answer isn't 3?"

A visual explanation of why the answer is 3+1.

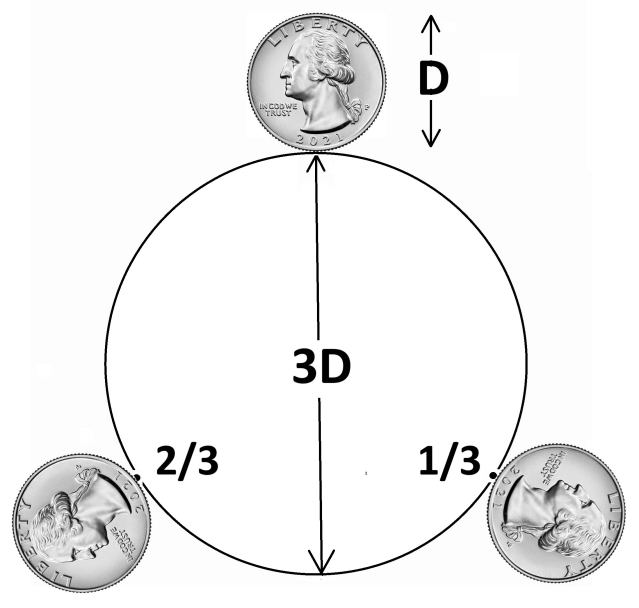
What should have happened next was a discussion of why 4 was the correct answer, but Jim was far too arrogant and just immediately storms out of my office without a chance for me to give an explanation. He should have first asked if I had heard the answer previously. He could then have asked for an explanation of why I came up with the answer, and so immediately. But he wasn't remotely interested in any of that. He was just angry that someone else had outsmarted him.

At the right is a visual explanation for the solution. When the quarter rotates 1/3rd the distance of the circumference, it's actually rotated one full rotation plus an extra 120°. The next rotation it gets to 2/3rds the distance so another full rotation plus another 120° so an additional 240°. The final 1/3rd brings the quarter back to the top, another full rotation plus 120°. So 3 rotations plus and additional 360° which is exactly one rotation.

But I wasn't really thinking of that solution because in actuality I had a big edge. The reason I knew it was 4 because I was into astronomy and there's a similiar problem with the Earth orbiting the Sun.

How many times does the Earth rotate around the Sun in a complete orbit? We all know that a day is exactly 24 hours, but that is more precisely called a Solar Day because it's the time (on average) that the Sun returns to the meridian. So you would logically think it's 365.24219 times. But that 24 hours is not one rotation of the Earth because we're also orbiting. The Earth rotates around its axis in 23 hours, 56 minutes, 4.0905 seconds (a Sidereal Day). But in a full year the Earth returns to the same point in its orbit. It has rotated exactly one more time! So the actual answer is really 366.24219 times. So when I saw the quarter rotation I knew it would also rotate exactly one more time so the number of rotations would be 4.

That was the last time Jim ever asked me about a problem in the remaining 10 years of my employment.

I've thought about the what if. What if I was taking that SAT test and had to answer that question. I believe I would have been bewildered and it would have cost me a bit of extra time, but I think I would have figured out that the test designers had got too cute. It was a pretty basic problem and they outsmarted themselves by using this description. I've since learned that there were only 3 students who complained to the SAT about the error, and all three of them did put down the answer 3 because they, too, figured that was the answer they were looking for, even though it was wrong. In an alternate universe, I took that test and then complained about it to the SAT.